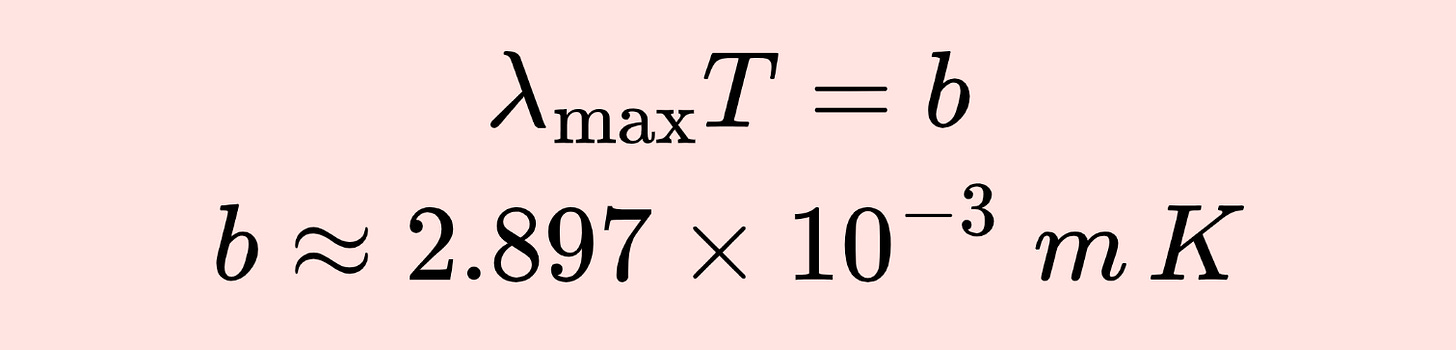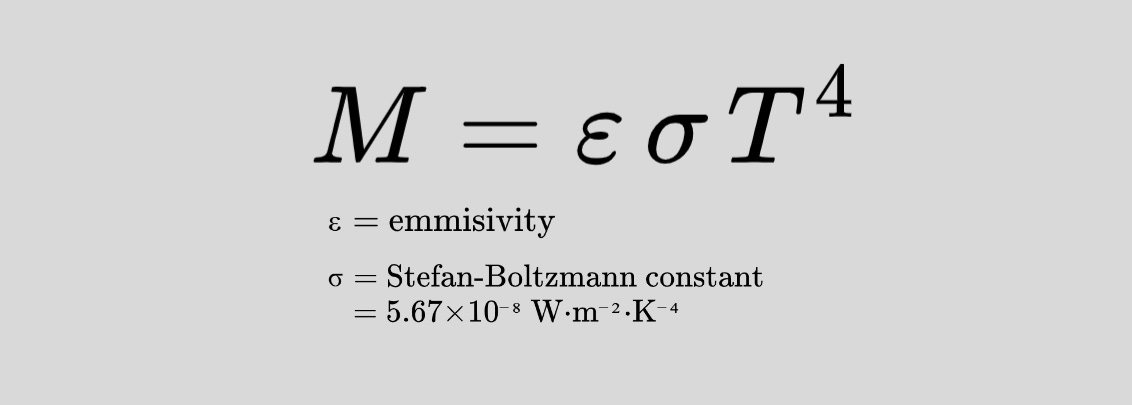How Max Planck inadvertently kickstarted the Quantum Revolution
The story of the mystical Black Body Radiation
Greetings, fellow Bohron.
‘A new scientific truth does not triumph by convincing its opponents and making them see the light, but rather because its opponents eventually die, and a new generation grows up that is familiar with it.
Max Planck wrote these words in the twilight of his life, reflecting on a career that had reshaped physics. Back in December 1900, Planck unveiled his groundbreaking equation describing the distribution of radiation from a black body—a discovery that marked the dawn of quantum theory.
But history is rarely the work of one mind alone. So, who were the other brilliant thinkers whose combined efforts propelled us into this new era of physics? It’s time for a science history lesson.
The Blackbody
An object heated to a high enough temperature emits both heat and light, whose intensity and color vary with the temperature.

The term ‘blackbody’ was first conceived in 1859 by German physicist Gustav Kirchhoff at Heidelberg University.
A blackbody is defined as a perfect absorber and emitter of radiation. The sun is a real-world approximation of an ideal blackbody.
He imagined his ideal blackbody to be a simple, insulated hollow container with a tiny hole in one of its walls. The hole acts as a perfect emitter and absorber of light (and therefore is the real blackbody). Any radiation entering the container through the hole is reflected back and forth between the walls of the cavity until it is completely absorbed. When heated, only the inner surface of the walls emits radiation.
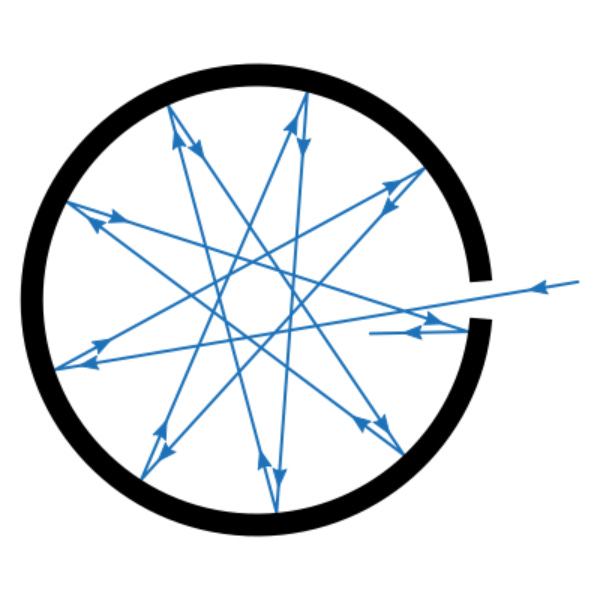
Kirchhoff showed that the range and intensity of the radiation emitted by the blackbody were independent of the nature of the body’s material, its shape, and size, but only dependent on its temperature. So the blackbody problem was reduced to this:
Measure the amount of energy at each wavelength at a given temperature.
Then derive a formula to reproduce the distribution at any temperature.

Devising a real blackbody wasn’t an easy task. Due to technical difficulties, the progress was halted for several decades.
Wien’s Law
In February 1893, Wilhelm Wien found that the temperature of a blackbody was inversely proportional to the wavelength at which it emits the radiation with the highest intensity. Essentially, Wien’s ‘displacement law’ stated that
the product of these two quantities was a constant.
This reduced the blackbody problem to calculating the value of this constant. In 1896, Wien wrote down an expression for the distribution of blackbody radiation.

Lummer and Pringsheim Experiments
Now it was up to Otto Lummer, along with Ferdinand Kurlbaum and Ernst Pringsheim, to put Wien’s law to the test. In 1898, they finally succeeded in designing a working electrically heated blackbody capable of reaching temperatures as high as 1500°C.
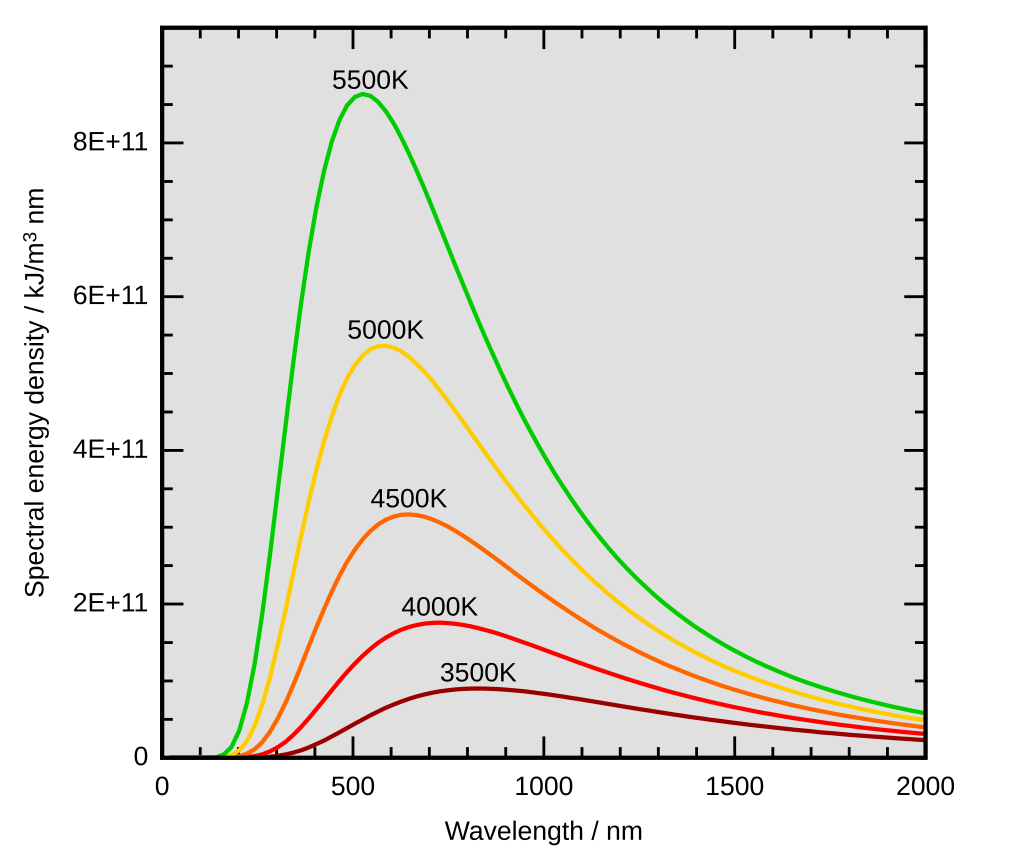
Intensity of radiation (on y-axis) was plotted against the wavelength of the radiation (on x-axis). The notable following features in their plot were:
The intensity rose as the wavelength of radiation increased up to a point, beyond which it began to drop.
The spectral energy distribution of blackbody radiation was almost a bell-shaped curve. The higher the temperature, the more pronounced the shape as the intensity of radiation emitted increased.
With increasing temperature, the peak wavelength that radiated with maximum intensity was displaced towards the ultraviolet end of the spectrum.
Wien’s law perfectly agreed with the observations at short wavelengths. However, it consistently overestimated the intensity of radiation at long wavelengths, where the Rayleigh-Jeans formula behaved better.
Lummer and Pringsheim reported their results at the meetings of the German Physical Society (GPS) held in Berlin on 3 February 1899, beginning of November 1899, and 2 February 1900. These meetings were also attended by Planck.
During the summer of 1900, Heinrich Rubens tested Wien’s law between wavelengths of 0.03 mm and 0.06 mm in the temperature range 200 to 1500°C. Again, the discrepancies were found at these longer wavelengths. In late September 1900, the failure of Wien’s Law was confirmed.
Planck begins his hunt
On the evening of Sunday, 7 October 1900, Max Planck was determined to find a formula that accurately described the energy spectrum of blackbody radiation. After several failed attempts, he arrived—through a mix of intuition and inspired guesswork—at a mathematical expression that seemed to fit the observed data. He shared it with Heinrich Rubens, who, a few days later, confirmed that Planck’s formula matched experimental results precisely. Planck presented this breakthrough at a meeting of the German Physical Society on Tuesday, 9 October 1900.

But what did the formula actually mean? The mathematics worked, but the physics behind it was a mystery. Planck later recalled,
“For this reason, on the very first day when I formulated this law, I began to devote myself to the task of investing it with true physical meaning.”
Over the next six weeks, he struggled to reconcile his equation with the reigning pillars of 19th-century physics—thermodynamics and electromagnetism. He couldn’t. Driven to the edge in his search for understanding, Planck made what he would later call “an act of desperation.” In doing so, he unknowingly took the first step into a new world: the quantum.
From Formula to Fundamentals
From electromagnetic theory, Planck knew that an oscillating electric charge emits and absorbs radiation only at its own frequency. Based on this, he modeled the walls of a blackbody as a vast ensemble of oscillators, each vibrating at a specific frequency. Individually, each oscillator contributed radiation at just one frequency—but together, they accounted for the full spectrum of blackbody radiation.
Planck imagined his array of oscillators as massless springs of varying stiffness—each with an electric charge attached—to account for the range of frequencies. Heating the walls of the blackbody supplied the energy needed to set these oscillators in motion. Whether a given oscillator became active depended solely on the temperature. Once active, it would both emit radiation into the cavity and absorb radiation from it. Over time, as this continuous exchange of energy unfolded, the system settled into balance. With the temperature held constant, the radiation and oscillators reached a state of thermal equilibrium.
Because the spectral energy distribution of blackbody radiation reflects how energy is spread across different frequencies, Planck assumed that the key lay in how many oscillators existed at each frequency. But as he worked through the problem, he realized—painfully—that the classical physics he had long trusted offered no path to his formula. In a moment of desperation, he turned to the unconventional ideas of the Austrian physicist Ludwig Boltzmann.
Boltzmann Comes to the Rescue
In 1884, Ludwig Boltzmann gave a theoretical foundation to a discovery made by his former mentor, Josef Stefan—that the total energy radiated by a blackbody is proportional to the fourth power of its temperature (T⁴). This relationship is now known as the Stefan-Boltzmann Law.
In the 1870s, Ludwig Boltzmann developed a statistical interpretation of the second law of thermodynamics, linking entropy with disorder. According to this view, the state of maximum entropy—maximum disorder—is simply the most probable state a system can occupy. For a blackbody, that state corresponds to thermal equilibrium.
If a blackbody contains 1,000 oscillators and ten of them resonate at a particular frequency, it is those ten that determine the intensity of radiation at that frequency. While the frequency of each of Planck’s electric oscillators is fixed, the energy it emits or absorbs depends entirely on its amplitude.

Hence Came The Quanta
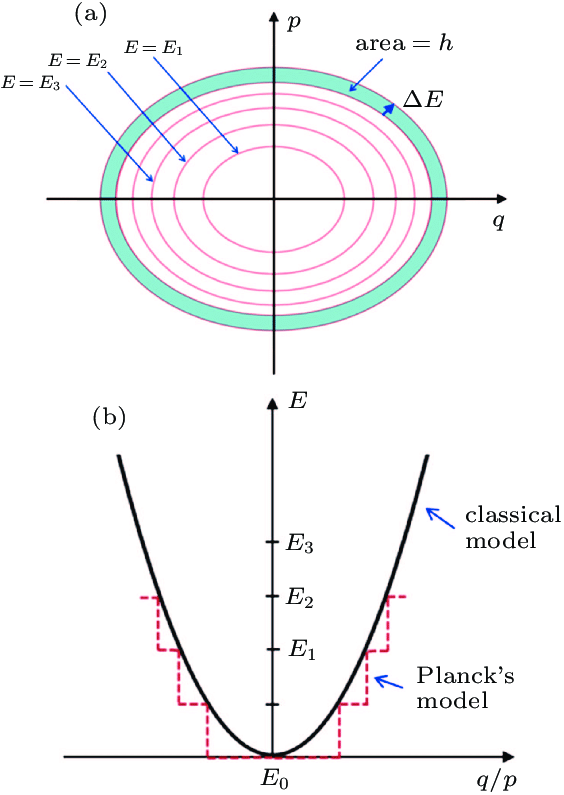
By applying Boltzmann’s statistical methods, Planck discovered that he could derive the correct formula for blackbody radiation only if he assumed that oscillators emitted and absorbed energy in discrete packets—each proportional to the frequency of oscillation. At any given frequency, energy had to be thought of as composed of equal, indivisible units—what Planck would later call quanta.
This led him to a radical step: slicing energy (E) into chunks of size hv, where vvv is the oscillator’s frequency and h is a new fundamental constant. Using Boltzmann’s approach, Planck calculated the most probable way to distribute these energy quanta among the oscillators. Since these oscillators could not possess arbitrary energy values, their amplitudes—and thus their behavior—were fundamentally constrained.
On 14 December 1900, at a GPS meeting, Planck unveiled this groundbreaking idea: a derivation of blackbody radiation based on the quantization of energy.
The Aftermath
In 1905 and 1906, Planck nominated Boltzmann for the Nobel Prize, recognizing the profound impact of his work. But privately, Boltzmann had been battling depression and chronic health issues for years. He felt that his life’s work—especially his statistical interpretation of thermodynamics—had been dismissed or ignored by much of the scientific community.
In September 1906, while on holiday in Duino near Trieste, Boltzmann took his own life. He was 62. His death came as a profound and tragic shock to the world of physics.

In deriving his formula, Planck had uncovered two new fundamental constants: k, which he named Boltzmann’s constant, and h, which he called the quantum of action—though it would soon be known to the world as Planck’s constant.
Yet despite this breakthrough, Planck regarded the notion of energy quanta as little more than a mathematical device—a strange but necessary trick to make the theory work. He was, in many ways, a reluctant revolutionary, unaware that he had just opened the door to an entirely new era in physics. Hesitant to assign any physical reality to his quanta, Planck held tightly to classical notions.
The first to boldly take that next step—to give Planck’s quanta real, physical meaning—was a young man living quietly in Bern, Switzerland.
References:
Ch 1: The Reluctant Revolutionary, Quantum, Manjit Kumar